Нарисуем на клетчатой бумаге какой-нибудь многоугольник. Например, такой, как показан на рисунке 1.

Попробуем теперь рассчитать его площадь. Как это сделать? Наверное, проще всего разбить его на прямоугольные треугольники и прямоугольники, площади которых уже нетрудно вычислить и сложить полученные результаты. Использованный мною способ несложен, но очень громоздок, кроме того он годится не для всяких многоугольников.

Рассмотрим невырожденный простой целочисленный многоугольник (т.е. он связный -- любые две его точки могут быть соединены непрерывной кривой, целиком в нем содержащейся, и все его вершины имеют целые координаты, его граница -- связная ломаная без самопересечений, и он имеет ненулевую площадь). Для вычисления площади такого многоугольника можно воспользоваться следующей теоремой:

Теорема Пика. Пусть -- число целочисленных точек внутри многоугольника, -- количество целочисленных точек на его границе, -- его площадь. Тогда справедлива формула Пика :

Пример. Для многоугольника на рисунке 1 (желтые точки), (синие точки, не забудьте о вершинах!), поэтому квадратных единиц.

Доказательство теоремы Пика. Сначала заметим, что формула Пика верна для единичного квадрата. Действительно, в этом случае мы имеем и

Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны и. Имеем в этом случае и, по формуле Пика,

Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами и, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат целочисленных точек. Тогда для этого случая и получаем, что

Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников и, возможно, прямоугольник (см. рисунки 2 и 3). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.

Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой многоугольник можно разбить на треугольники (например, диагоналями). Поэтому нужно просто доказать, что при добавлении любого треугольника к произвольному многоугольнику формула Пика остается верной.

Пусть многоугольник и треугольник имеют общую сторону. Предположим, что для формула Пика справедлива, докажем, что она будет верна и для многоугольника, полученного из добавлением. Так как и имеют общую сторону, то все целочисленные точки, лежащие на этой стороне, кроме двух вершин, становятся внутренними точками нового многоугольника. Вершины же будут граничными точками. Обозначим число общих точек через и получим

Число внутренних целочисленных точек нового многоугольника,

Число граничных точек нового многоугольника.

Из этих равенств получаем

Так как мы предположили, что теорема верна для и для по отдельности, то

Тем самым, формула Пика доказана.

Эту формулу открыл австрийский математик Пик Георг Александров (1859 - 1943 г.г.) в 1899 году. Кроме этой формулы Георг Пик открыл теоремы Пика, Пика - Жюлиа, Пика - Невалины, доказал неравенство Шварца - Пика. В Приложении 1 можно увидеть рассмотренные мною нестандартные задачи на применение формулы Пика.

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Выполнила ученица МОУ СОШ №7 8 «А» класса Юношева Ксения Преподаватель: Бабина Наталья Алексеевна г. Сальск 2011 год «Формула Пика»

Цели работы: Выяснение существования иной, отличной от школьной программы, формулы нахождения площади решетчатого многоугольника. Области применения искомой формулы.

Введение. Математическое образование, получаемое в общеобразовательных школах, является важнейшим компонентом общего образования и общей культуры современного человека. На данном этапе, школьная система рассчитана на одиннадцатилетнее обучение. Всем учащимся в конце одиннадцатого класса предстоит сдавать Единый Государственный Экзамен, который покажет уровень знаний, полученный во время учебы в школе. Но школьная программа не всегда предоставляет самые рациональные способы решения каких-либо задач. Например, просматривая результаты ЕГЭ 2010 года видно, что многие ученики теряют баллы из-за задания В6. Я задалась целью, как же можно сэкономить время и правильно решить это задание.

Задание В6. На клетчатой бумаге с клетками размером 1 см на 1 см изображены фигуры(см. рисунок). Найдите их площади в квадратных сантиметрах.

Итак, чтобы все-таки решить это задание мне нужно применить формулы нахождения площади, которые мы изучаем в 8классе.Но на это уйдет очень много времени, а мне нужно ответить на поставленный вопрос как можно быстрее, ведь время на экзамене строго ограниченно. Поэтому, проведя исследования, я выяснила, что существует теорема Пика, которая в школьной программе не изучается, но которая поможет мне быстрее справиться с заданием.

Историческая справка. Георг Александр Пик (10 августа, 1859 - 26 июля 1942) был австрийским математиком. Он умер в концлагере Терезин. Сегодня он известен из-за формулы Пика для определения площади решетки полигонов. Он опубликовал свою формулу в статье в 1899 году, она стала популярной, когда Хьюго Штейнгауз включил её в 1969 году в издание математических снимков. Пик учился в Венском университете и защитил кандидатскую в 1880 году. После получения докторской степени он был назначен помощником Эрнеста Маха в Шерльско-Фердинандском университете в Праге. Он стал преподавателем там в 1881 году. Взяв отпуск в университете в 1884 году, стал работать с Феликсом Клейном в Лейпцигском университете. Он оставался в Праге до своей отставки в 1927 году, а за тем вернулся в Вену. Пик возглавлял комитет в(тогда) немецком университете Праги, который назначил Альберта Эйнштейна профессором кафедры математической физики в 1911 году. Пик был избран членом Чешской академии наук и искусств, но был исключен после захвата нацистами Праги. После ухода на пенсию в 1927 году, Пик вернулся в Вену, город, где он родился. После аншлюса, когда нацисты вошли в Австрию 12 марта 1938 года, Пик вернулся в Прагу. В марте 1939 года нацисты вторглись в Чехословакию. Георг был отправлен в концентрационный лагерь Терезин 13 июля 1942. Он умер через две недели.

Теорема Пика. Теорема Пика - классический результат комбинаторной геометрии и геометрии чисел. Площадь многоугольника с целочисленными вершинами равна сумме В + Г/2 – 1, где В есть количество целочисленных точек внутри многоугольника, а Г количество целочисленных точек на границе многоугольника.

Доказате льст во теоремы Пика. Любой такой многоугольник легко разбить на треугольники с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах. Можно показать, что площади всех этих треугольников одинаковы и равны 1/2, а, следовательно, площадь многоугольника равна половине их числа Т. Чтобы найти это число, обозначим через п число сторон многоугольника, через i - число узлов внутри его и через b - число узлов на сторонах, включая вершины. Общая сумма углов всех треугольников равна πТ. Теперь найдём эту сумму другим способом. Сумма углов с вершиной в любом внутреннем узле составляет 2 π , т. е. общая сумма таких углов равна 2 π i ; общая сумма углов при узлах на сторонах, но не в вершинах равна (b – n) π , а сумма углов при вершинах многоугольника - (п – 2) π . Таким образом, π Т = 2i π + (b – n) π + (n – 2) π , откуда получаем выражение для площади S многоугольника, известное как формула Пика. Например, на рисунке b = 9, i = 24, а следовательно, площадь многоугольника равна 27,5.

Применение. Итак, вернемся к заданию В6. Теперь, зная новую формулы, мы легко сможем найти площадь этого четырехугольника. Так как В – 5; Г – 14, то 5+14:2-1=11 (см в квадрате) Площадь данного четырехугольника равна 11 см в квадрате.

По той же формуле мы можем найти площадь треугольника. Так как В-14, Г-10,то 14+10:2-1=18 (см в квадрате) Площадь данного треугольника равна 18 см в квадрате.

Если В-9, Г-12, тогда: 9+12:2-1=14 (см в квадрате) Площадь данного четырехугольника равна 14 см в квадрате.

Области применения формулы. Помимо того, что формула применяется в различного рода экзаменах, заданиях и так далее, она сопровождает весь окружающий нас мир.

По формуле Пика S =В + ½ Г-1 1)туловище В=9,Г=26, S=9+½·26-1=9+13-1= 21 2) хвост В=0,Г=8, S= 0 +½· 8 -1= 3 3) S= 21+3=24

По формуле Пика S =В + ½ Г-1 В=36, Г=21 S = 36 + ½· 21 -1=36+10,5-1=45,5

Заключение. В итоге, я пришла к выводу, что существует много различных способов решения задач на нахождение площади, не изучаемых в школьной программе, и показала их на примере формулы Пика.

Справочник. Многоугольник без самопересечений называется решётчатым, если все его вершины находятся в точках с целочисленными координатами (в декартовой системе координат). Точка координатной плоскости называется целочисленной, если обе её координаты целые.

В Викисловаре есть статья «пика» Пика В военном деле: Пика холодное колющее оружие, разновидность длинного копья. Пикинёры вид пехоты в европейских армиях XVI начала XVIII веков. Пикельхельм (п … Википедия

Теорема Пика (комбинаторная геометрия) - В=7, Г=8, В + Г/2 − 1= 10 Теорема Пика классический результат комбинаторной геометрии и геометрии чисел. Площадь многоугольника с целочисле … Википедия

Треугольник - У этого термина существуют и другие значения, см. Треугольник (значения). Треугольник (в евклидовом пространстве) это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки,… … Википедия

Трапеция - У этого термина существуют и другие значения, см. Трапеция (значения). Трапеция (от др. греч. τραπέζιον «столик»; … Википедия

Четырёхугольник - ЧЕТЫРЁХУГОЛЬНИКИ ┌─────────────┼────────────┐ невыпуклый выпуклый самопересекающийся … Википедия

Двуугольник - Правильный двуугольник на поверхности сферы Двуугольник в геометрии это … Википедия

Пятиугольник - Правильный пятиугольник (пентагон) Пятиугольник многоугольник с пятью углами. Также пятиугольником называют всякий предмет такой формы. Сумма внут … Википедия

Шестиугольник - Правильный шестиугольник Шестиугольник многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы. Сумма внутренних углов выпуклого шестиугольника р … Википедия

Додекагон - Правильный додекагон Додекагон (греч … Википедия

Прямоугольник - Прямоугольник параллелограмм, у которого все углы прямые (равны 90 градусам). Примечание. В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые. Четвёртый угол (в силу … Википедия

Книги

• Математический клуб «Кенгуру». Выпуск № 8. Математика на клетчатой бумаге , . Выпуск посвящен различным задачам и играм, связанным с листом клетчатой бумаги. В частности, в нем подробно рассматривается вычисление площади многоугольника, вершины которого расположены в…

Формула Пика

1. Введение

2. Формула Пика. Доказательство I .

Доказательство II .

Доказательство Ш.

3. Задачи.

4. Формула площади многоугольника через координаты вершин.

5. Задачи.

6. Литература

Формула Пика.

1. Введение.

В истории черпаем мы мудрость,

в поэзии - остроумие,

в математике - проницательность.

Ф. Бэкон

Сюжет будет разворачиваться на обычном листке клетчатой бумаги.

Линии, идущие по сторонам клеток, образуют сетку, а вершины клеток - узлы этой сетки. Нарисуем на листе многоугольник с вершинами в узлах и найдём его площадь.

Искать её можно по - разному. Например, можно разрезать многоугольник на достаточно простые фигуры, найти их площади и сложить.

Но тут нас ждёт много хлопот. Фигура легко разбивается на прямоугольники, трапеции, и треугольники, и её площадь вычисляется без усилий.

Хотя многоугольник и выглядит достаточно просто, для вычисления его площади придется изрядно потрудиться. А если бы многоугольник выглядел более причуд­ливо? Оказывается, площади многоугольни­ков, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с коли­чеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика.

2. Формула Пика.

Вершины многоугольника (не обязательно выпуклого) расположены в узлах целочисленной решетки. Внутри его лежит В узлов решетки, а на границе Г узлов. Докажем, что его площадь равна В + – 1 (формула Пика).

Доказательство I .

Рассмотрим многоугольник, вершины которого находятся в узлах целочисленной решётки, то есть имеют целочисленные координаты.

Многоугольник разобьём на треугольники с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах.

Обозначим:

n – число сторон многоугольника,

m – количество треугольников с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах,

В – число узлов внутри многоугольника,

Г – число узлов на сторонах, включая вершины.

Площади всех этих треугольников одинаковы и равны .

Следовательно, площадь многоугольника равна
.

180 0 m .

Теперь найдём эту сумму другим способом.

Сумма углов с вершиной в любом внутреннем узле составляет 360 0 .

Тогда сумма углов с вершинами во всех внутренних узлах равна 360 0 В.

Общая сумма углов при узлах на сторонах, но не в вершинах равна 180 0 (Г – n ).

Сумма углов при вершинах многоугольника равна 180 0 (n – 2) .

Общая сумма углов всех треугольников равна 360 0 В + 180 0 (Г – n ) + 180 0 (n – 2).

Таким образом, 180 0 m = 360 0 В + 180 0 (Г – n ) + 180 0 (n – 2),

180 0 m = 360 0 В + 180 0 Г – 180 0 n + 180 0 n – 180 0 ·2,

180 0 m = 360 0 В + 180 0 Г– 360 0 ,

= В + – 1 ,

откуда получаем выражение для площади S многоугольника:

S = В + – 1 ,

известное как формула Пика.

На рисунке: В = 24, Г = 9, следовательно, S = 24 + – 1 = 27,5.

Найдём площадь первого многоугольника по формуле Пика:

В = 28 (зеленые точки);

Г = 20 (синие точки).

Получаем, S =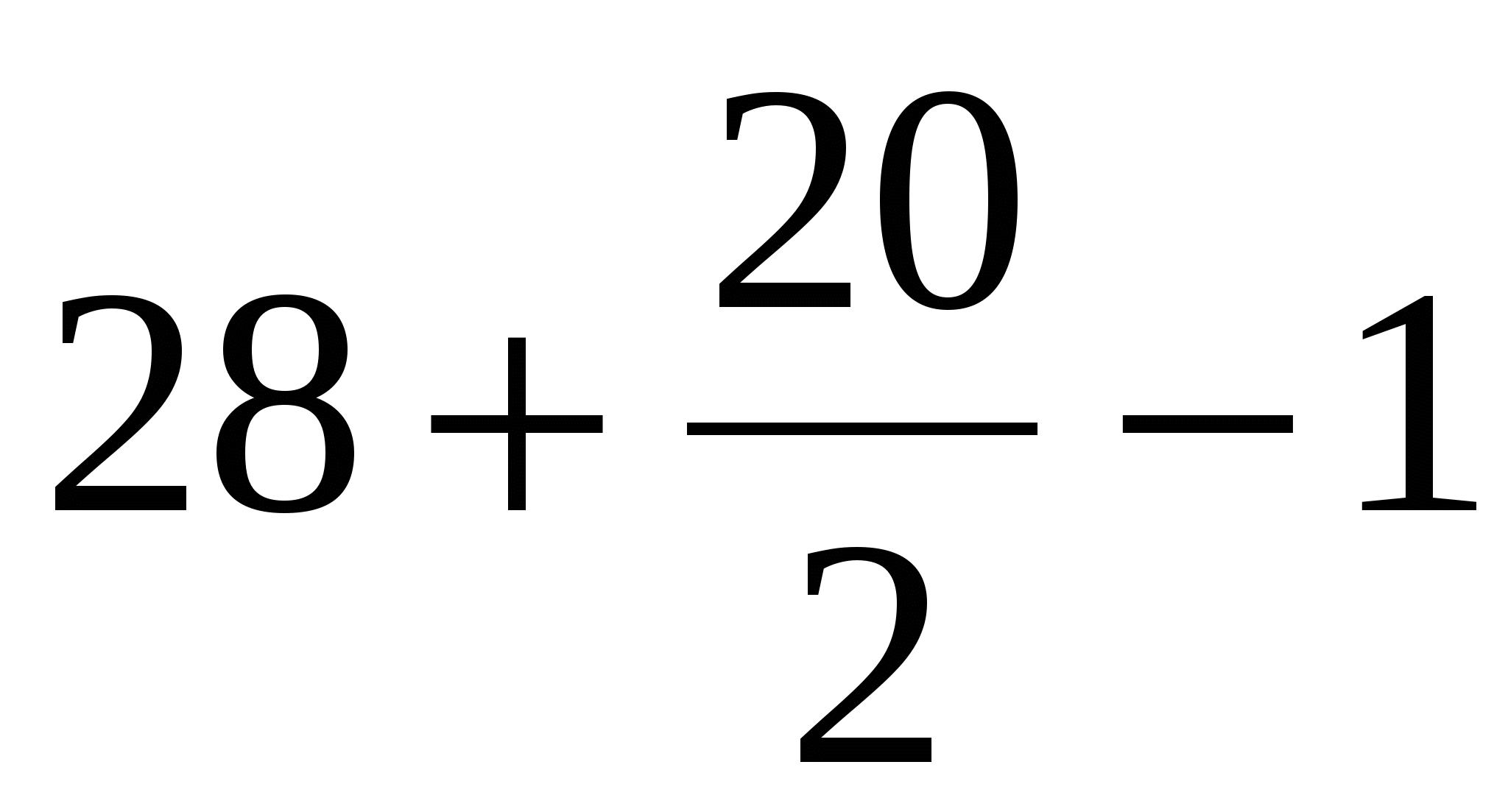
= 37 кв.ед.

Доказательство II .

Каждому многоугольнику M с вершинами в узлах целочисленной решетки поставим в соответствие число f (M) =
, где суммирование ведётся по всем узлам решётки, принадлежащим M, а угол определяется следующим образом: =
для внутренней точки многоугольника, =
для граничной точки, отличной от вершины, и – угол при вершине, если данный узел – вершина. Легко видеть, что f (M) =
+
= В + – 1. Остаётся проверить, что число f (M) равно площади многоугольника M.

Пусть многоугольник M разрезан на многоугольники M 1 и M 2 с вершинами в узлах решетки. Тогда f (M) = f (M 1) + f (M 2), поскольку для каждого узла углы складываются. Поэтому если формула Пика верна для двух из многоугольников M, M 1 и M 2 , то она верна и для третьего.

Если M - прямоугольник со сторонами p и q , направленными по линиям решетки, то

f (M) = (p – 1)(q – 1) +
= pq.

В этом случае формула Пика справедлива. Разрезав прямоугольник M диагональю на треугольники M 1 и M 2 и воспользовавшись тем, что f (M) = f (M 1) + f (M 2) и f (M 1) = f (M 2), легко доказать справедливость формулы Пика для любого прямоугольного треугольника с катетами, направленными по линиям решетки. Отрезав несколько таких треугольников от прямоугольника, можно получить любой треугольник.

Для завершения доказательства формулы Пика остается заметить, что любой многоугольник можно разрезать на треугольники непересекающимися диагоналями.

Доказательство Ш.

Связь между площадью фигуры и количе­ством узлов, попавших в эту фигуру, особенно ясно видна в случае прямоугольника.

Пусть ABCD - прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки.

Обозначим через В количество узлов, лежа­щих внутри прямоугольника, а через Г - ко­личество узлов на его границе. Сместим сетку на пол клетки вправо и полклетки вниз.

Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещенной сетки, каждый из Г – 4 гра­ничных неугловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S равна

Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, мы установили формулу

Докажем, что эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки.

Обозначим через S м площадь многоуголь­ника М с вершинами в узлах, а через П м – величину
, где В м – число узлов внутри М, а Г м - число узлов на границе. Тогда формулу Пика можно записать в виде
.

Доказательство формулы разобьем на не­сколько шагов.

Шаг 1.

Если многоугольник М с вершина­ми в узлах сетки разрезан на 2 многоугольни­ка М 1 и М 2 , также имеющих вершины только в узлах сетки, то
. Пусть многоугольник М разрезан на много­угольники М 1 и М 2 с вершинами в узлах отрез­ком АВ. Все узлы, кроме тех, которые попадают на отрезок АВ, дают одинаковый вклад в левую и правую части формулы. Рассмотрим узлы, лежащие на отрезке АВ.

Если такой узел лежит между А и В (на­пример, С), то для многоугольника М он внутренний, а для многоугольников М 1 и М 2 – граничный. Поэтому его вклад в П м равен 1, а в каждое из выражений
и
– по 0,5, то есть вклады такого узла в П м и
равны.

Рассмотрим узлы А и В. Они граничные как для М , так и для М 1 , М 2 .

Поэтому вклад каждого из этих узлов в П м равен 0,5 а в
- единице. Значит, суммарный вклад узлов А и В в П м равен 1, что на 1 меньше, чем их вклад в
. Но
, а .

Из общего «вклада» всех узлов П м вычи­тается 1, а из
вычитается 2, и это компенсирует разницу вкладов узлов А и В.

Итак,
.

Шаг 2.

Если многоугольник М с вершинами в узлах сетки разрезан на два многоугольника М 1 и М 2 (тоже с вершинами в узлах) и формула верна для каких-то двух из многоугольников М, М 1 , М 2 , то она верна и для третьего многоугольника.

Пусть, например, она верна для М 1 и М 2 , то есть
. Тогда (по первому шагу) , но (по перво­му шагу) последнее выражение равно П м , а равенство
и есть формула Пика.

Шаг 3.

Докажем формулу Пика для пря­моугольного треугольника с вершинами в узлах сетки и катетами, лежащими на линиях сетки.

Треугольник АВС достроим до прямоуголь­ника ABCD .

Для прямоугольников формула Пика верна: S ABCD = П ABCD . Согласно первому шагу П ABCD = П ABC + П ACD , П ABC = П ACD , так что П ABCD = 2П ABC . Но S ABCD = 2 S ABC . Поэтому S ABC = П ABC .

Шаг 4.

Формула Пика верна для произволь­ного треугольника с вершинами в узлах сетки.

Рассмотрев рисунок, легко понять: любой такой треугольник можно получить, «отрезав» от некоторого прямоугольника со сторонами, идущими по линиям сетки, несколько прямо­угольников и прямоугольных треугольников с катетами на линиях сетки. А так как формула Пика верна для прямоугольников и прямоугольных треугольников, то (вспомним шаг 2) она верна и для исходного треугольника.

Мы доказали, что если многоугольник мож­но разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.

3. Задачи.

Найдите площади фигур:

1
.

B = 9

Г = 4

B = 9

Г = 5